Q. What is the minimum number of rays required for locating the image formed by a convex mirror for an object ? Draw a ray diagram to show the formation of a virtual image by a convex mirror.
Q. Refractive index of diamond with respect to glass is 1.6 and absolute refractive index of glass is 1.5. Find (i) absolute refractive index of diamond (ii) Speed of light in diamond. The speed of light in air is 3x108 m/s.
A1B1 /AB = OA1/OA -------------------(i)
Q. A 4.0cm tall object is placed perpendicular to the principal axis of a convex lens of focal length 20cm. If the distance of the object from the lens is 30cm, find the position, nature and size of the image. Also, find its magnification.
Q. (a) 4.5cm needle is placed 12cm away from a convex mirror of focal length 15cm. Give the location of the image and the magnification. Describe what happens as the needle is moved farther from the mirror.
(b) What kind of mirror is used in a solar furnace ? Give reason for using this mirror.
(c) One half of a convex lens is covered with a black paper. Will this lens produce a complete image of the object ? Justify your answer.
Q. (a) When an object is placed at a distance of 60 cm from a convex mirror the magnification produced is 1/2 . Where should the object be placed to get a magnification of 1/3 ? (b) A small electric lamp is placed at the focus of a convex lens. What is the nature of beam of light produced by the lens. Draw a diagram to show this.
Q. The refractive index of a dense flint glass is 1.65 and for alcohol it is 1.36 with respect to air. Find the refractive index of dense flint glass with respect to alcohol.
Q. Draw a ray diagram to show refraction of light through a triangular glass prism and show angle of incidence and angle of deviation.
Q. Refractive index of diamond with respect to glass is 1.6 and absolute refractive index of glass is 1.5. Find (i) absolute refractive index of diamond (ii) Speed of light in diamond. The speed of light in air is 3x108 m/s.
Q. Name a mirror that can give an erect and magnified image of an object. Draw labelled ray diagram to justify your answer.
Q. (a) Define “power of accommodation of eye”.
(b) A person uses a lens of power -2.0D for correcting his distant vision. For correcting his near vision he uses a lens of power +1.5D. What is the focal length of the lenses required to correct this disorder ?
Q. (a) State Snell’s Law.
(b) A beam of light passes from air to a substance X. If angle of incidence is 45 degrees and angle of refraction is 30 degrees, calculate the refractive index of substance X. Given sin 30o = ½ ; sin 45 o = 1/rot2
(c) A convex lens forms a real and inverted image of a needle at a distance of 50 cm from it. Where is the needle placed if the size of the image is equal to the size of the object ? Calculate the power and focal length of the lens.
Q. (a) An object is placed at a distance of 60 cm from a convex mirror the magnification produced is 1/2 . Where should the object be placed to get a magnification of 1/3 ?
(b) A small electric lamp is placed at the focus of a convex lens. State the nature of beam of light produced by the lens. Draw a diagram to show this.
Q. The radius of curvature of concave mirror is 50cm. Where should an object be placed from the mirror so as to form its image at infinity ? Justify your answer.
Q. (a) Name and define the S.I. unit of power of a lens. (b) How is the power of a lens related to its focal length ? Find the power of a concave lens of focal length 25cm.
Q. (a) State Snell‟s law of refraction. (b) What is the speed of light in a transparent medium which has a refractive index of 1.7 (the speed of light in vacuum is 3x108 m/s)
Q. (a) Two lenses have power of (i) 2D (ii) – 4D. State the nature and focal length of each lens.
(b) A concave lens has focal length of 20 cm. At what distance from the lens a 5cm tall object be placed so that it forms an image at 15cm from the lens ? Also calculate the size of the image formed.
Q. (a) Name the type of mirror used in the following :
(i) Headlights of a car. (ii) Rear view mirror of a vehicle. Support your answer with reason.
(b) When an object is placed at a distance of 60cm from a diverging spherical mirror, the magnification produced is 0.5. Where should the object be placed to get a magnification of 1/3 ?
Q. An object is placed at a distance of 20 cm in front of convex mirror of radius of curvature 30 cm. Find the position and nature of the image.
Q. State the type of lens used as a simple magnifying glass. Draw a labelled ray diagram to show the image formation by this lens. List the characteristics of the image formed.
Q. (i) Find the value of the angle of reflection when an incident ray makes an angle of 40o with a plane mirror.
(ii) Light enters from air into water which has a refractive index of 1.33. Calculate the speed of light in water. (speed of light in air is 3 x 108 m/s.)
Q. Draw a ray diagram in each of the following cases to show the position and nature of the image formed when the object is placed
(i) between pole and principal focus of a concave mirror.
(ii) between centre of curvature and principal focus of a concave mirror.
Name the type of mirror which can be used to obtain a diminished and virtual image of an object. Mention an application of such a mirror . Draw a labelled ray diagram to show the formation of the required image in the mirror.
Q. Name the type of lens that can be used to obtain :
(i) A magnified and virtual image. (ii) A diminished and virtual image of the object.
Draw labelled ray diagrams to show the formation of the required image in each of the above two cases. Which of these lenses can also form a magnified and real image of the object? Draw labelled ray diagram to show the position of object and image for such a lens.
Q. (i) List any two properties of the image formed by a plane mirror. (ii) The power of a spherical lens is – 2D. State its nature and calculate its focal length in centimeter.
Q. (i) Define optical centre of a lens.
(ii) In refraction of light through a rectangular glass slab, the emergent ray is parallel to the direction of the incident ray. Why ?
(iii) What happens when a light ray is incident normally on one of the faces of a rectangular glass slab ?
Q. (i) Draw a ray diagram in each of the following cases. Also mark the angle of incidence
(i) and angle of reflection in the diagram.
(a) A ray passing through the principal focus of a convex mirror.
(b) A ray incident obliquely to the principal axis towards the pole of a concave mirror.
(ii) An object, 2.0 cm in size, is placed 20.0cm in front of a concave mirror of focal length 15.0cm. At what distance from the mirror should a screen be placed in order to obtain a sharp image ? Find the nature and the size of the image formed.
Q. (i) Draw the ray diagrams in each of the following cases to show the position and nature of the image formed when the object is placed :
(a) at „2F‟ of a converging lens. (b) between the focus and optical centre of a converging lens.
(ii) The magnification produced by a spherical lens is 1/3 . If the image is formed at a distance of 10cm from the lens, find the position of object. Also find the nature and focal length of this lens.
Q. A 2 cm tall object is placed at a distance of 25 cm from a convex lens of focal length 10 cm. Find the nature, size and position of the image so formed.
Q. With respect to air the refractive index of kerosene is 1.44 and that of diamond is 2.42. Calculate the refractive index of diamond with respect to kerosene
Q. Name the type of mirror which always forms a virtual and diminished image of the object in front of it. Draw the diagram for the same for an object in front of it at a finite distance. State any one use of it
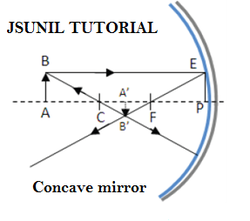
Derivation or Proof of Mirror and lens formula CBSE(X) physics
Mirror formula is the relationship between object distance (u), image distance (v) and focal length.
1/v + 1/u = 1/f
In D ABC and D A’B’C
D ABC ~ D A’B’C [AA similarity]
AB /A’B’ = AC/A’C ----(I)
Similarly,
In DABC and D A’B’C
D ABC ~ DA’B’C [AA similarity]
AB /A’B’ = AC/A’C ----(1)
Similarly, In D FPE ~ D A’B’F
EP /A’B’ = PF/A’F
AB /A’B’ = PF/A’F [ AB=EP] ----(II)
From (i) &(ii)
AC/A’C = PF/A’F
=> A’C/AC = A’F/PF
=> (CP-A’P)/(AP- CP) = (A’P – PF)/PF
Now, PF = - f ; CP = 2PF = -2f ; AP = -u ; and A’P = -v
Put these value in above relation:
[(-2f) –(-v)] /(-u)-(-2f) = {(-v) –(-f) }/(-f)
=> uv = fv +uf
=> 1/f = 1/u + 1/v
Let AB is an object placed between f1 and f2 of the convex lens. The image A1B1 is formed beyond 2F2 and is real and inverted.
OA = Object distance = u ; OA1 = Image distance = v ; OF2 = Focal length = f
In D OAB and D OA1B1
A1B1 /AB = OA1/OA -------------------(i)
Similarly, D OCF2 ~ D F2A1B1
A1B1 /OC = F2A1/OF2
But we know that OC = AB
=> A1B1 /AB = F2A1/OF2 -------------------(ii)
From equation (i) and (ii), we get
OA1/OA = F2A1/OF2
OA1/OA = (OA1 - OF2)/OF2
v/-u = (v-u)/f
vf = -u(v-f)
vf = -uv + uf
Dividing equation (3) throughout by uvf
1/v - 1/u = 1/f
can someone give me the solutions for these question?
ReplyDelete